AVL Trees

AVL Tree Definition

• AVL trees are balanced.
• An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by at most 1.

Height of an AVL Tree

• Fact: The height of an AVL tree storing n keys is O(log n).
• Proof: Let us bound n(h): the minimum number of internal nodes of an AVL tree of height h.
• We easily see that n(1) = 1 and n(2) = 2
• For n > 2, an AVL tree of height h contains the root node, one AVL subtree of height n-1 and another of height n-2.
• That is, n(h) = 1 + n(h-1) + n(h-2)
• Knowing n(h-1) > n(h-2), we get n(h) > 2n(h-2). So n(h) > 2n(h-2), n(h) > 4n(h-4), n(h) > 8n(n-6), … (by induction), n(h) > 2in(h-2i)
• Solving the base case we get: n(h) > 2^(h/2-1)
• Taking logarithms: h < 2log n(h) +2
• Thus the height of an AVL tree is O(log n)

Insertion

• Insertion is as in a binary search tree
• Always done by expanding an external node.
• Afterwards Restructuring

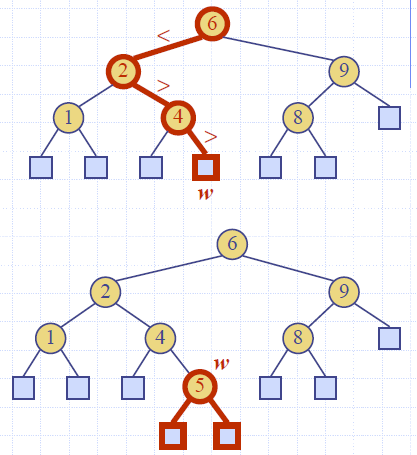
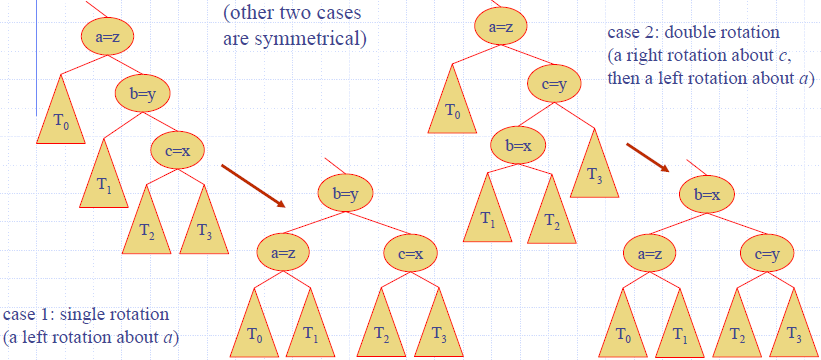
Trinode Restructuring

• let (a,b,c) be an inorder listing of x, y, z
• perform the rotations needed to make b the topmost node of the three

Removal

• Removal begins as in a binary search tree, which means the node removed will become an empty external node. Its parent, w, may cause an imbalance. *

Rebalancing after a Removal

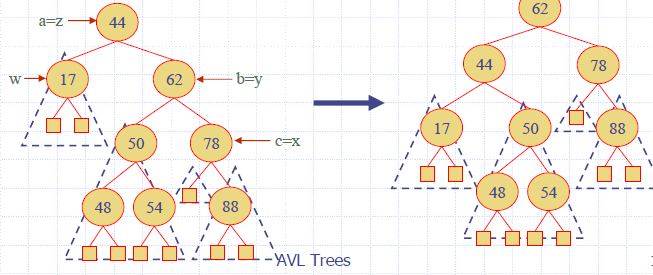
• Let z be the first unbalanced node encountered while travelling up the tree from w. Also, let y be the child of z with the larger height, and let x be the child of y with the larger height.
• We perform restructure(x) to restore balance at z.
• As this restructuring may upset the balance of another node higher in the tree, we must continue checking for balance until the root of T is reached

Running Times

• a single restructure is O(1) using a linked-structure binary tree
• find is O(log n) height of tree is O(log n), no restructures needed
• insert is O(log n)
  • initial find is O(log n)
  • Restructuring up the tree, maintaining heights is O(log n)
• remove is O(log n)
  • initial find is O(log n)
  • Restructuring up the tree, maintaining heights is O(log n)

Code

/**
 *
 */
package examples;

import java.util.ArrayList;
import java.util.Iterator;
import java.util.Map;
import java.util.Random;
import java.util.TreeMap;

import com.sun.javafx.css.CascadingStyle;

/**
 * @author ps
 *
 */
public class MyAVLTree<K extends Comparable<? super K>, E> implements
        OrderedDictionary<K, E> {

    class AVLNode implements Locator<K, E>{

        AVLNode parent,left,right;
        Object creator = MyAVLTree.this;
        E elem;
        K key;
        int height;

        /* (non-Javadoc)
         * @see examples.Position#element()
         */
        @Override
        public E element() {
            return elem;
        }

        /* (non-Javadoc)
         * @see examples.Locator#key()
         */
        @Override
        public K key() {
            return key;
        }

        boolean isExternal(){
            return left==null; // is also true for right
        }

        boolean isLeftChild(){
            return parent != null && parent.left==this;
        }

        boolean isRightChild(){
            return parent != null && parent.right==this;
        }

        void expand(K key,E elem){
            this.elem = elem;
            this.key = key;
            left = new AVLNode();
            right = new AVLNode();
            left.parent = this;
            right.parent = this;
            height = 1;
        }
    }



    // istance variables:
    private AVLNode root = new AVLNode();
    private int size;

    private AVLNode checkAndCast(Locator<K,E> p){
        try {
            AVLNode n = (AVLNode) p;            
            if (n.creator == null) throw new RuntimeException(" allready removed locator!");
            if (n.creator != this) throw new RuntimeException(" locator belongs to another AVLTree instance");
            return n;
        } catch (ClassCastException e) {
            throw new RuntimeException(" locator belongs to another container-type ");
        }
    }



    @Override
    public int size() {
        return size;
    }




    @Override
    public Locator<K, E> find(K key) {
        AVLNode n = root;
        AVLNode found = null;
        while ( ! n.isExternal()){
            int comp = key.compareTo(n.key);
            if (comp < 0) n = n.left;
            else if (comp > 0) n=n.right;
            else {
                found = n;
                n=n.left;
            }            
        }
        return found;
    }




    @Override
    public Locator<K, E>[] findAll(K key) {
        AVLNode n = (AVLNode)find(key);
        if (n==null) return (Locator<K,E>[]) new Locator[0];
        List<AVLNode> list = new MyLinkedList<>();
        while(n!=null && n.key.equals(key)) {
            list.insertLast(n);
            n= (AVLNode ) next(n);
        }
        Iterator<AVLNode> it = list.elements();
        Locator[] ret = new Locator[list.size()];
        for(int i=0;i<ret.length;i++) ret[i]=it.next();
        return ret;
    }


    @Override
    public Locator<K, E> insert(K key, E o) {
        AVLNode n = root;
        while ( ! n.isExternal()){
            if (key.compareTo(n.key) < 0){
                n=n.left;
            }
            else n = n.right;
        }
        n.expand(key,o);
        size++;
        adjustHeightAboveAndRebalance(n);
        return n;
    }




    private void adjustHeightAboveAndRebalance(AVLNode n) {
        n = n.parent;
        while (n != null ){
            int newHeight = Math.max(n.left.height,n.right.height)+1;
            boolean balanced = Math.abs(n.left.height-n.right.height)<2;
            if (balanced && newHeight == n.height) break;
            n.height = newHeight;
            if ( ! balanced) n = restructure(n);                
            n = n.parent;
        }
    }



    @Override
    public void remove(Locator<K, E> loc) {
        AVLNode n = checkAndCast(loc);
        AVLNode w;      // is the node which replaced
                        // the one we removed really

        if (! n.left.isExternal() && ! n.right.isExternal()) {
            // we find the most left node in the right subtree
            AVLNode r;
            if (n.right.height > n.left.height){
                r = n.right;
                while ( ! r.left.isExternal()) r = r.left;
            }
            else {
                r=n.left;
                while ( ! r.right.isExternal()) r = r.right;
            }
            w = removeAboveExternal(r);
            // now we have to replace n by r
            r.parent = n.parent;
            if (n==root) root = r;
            else {
                if (n.isLeftChild()) n.parent.left = r;
                else  n.parent.right = r;
            }
            r.height = n.height;
            r.left = n.left;
            r.right = n.right;
            r.right.parent = r;
            r.left.parent = r;

        }
        else w = removeAboveExternal(n);
        n.creator = null;
        size--;
        adjustHeightAboveAndRebalance(w);
    }

    private AVLNode removeAboveExternal(AVLNode n) {
        AVLNode w;
        if (n.left.isExternal()){
            w = n.right;
            w.parent = n.parent;
            if (n.isLeftChild()) w.parent.left = w;
            else if (n.isRightChild()) w.parent.right = w;
            else root = w;
        }
        else {
            w = n.left;
            w.parent = n.parent;
            if (n.isLeftChild()) w.parent.left = w;
            else if (n.isRightChild()) w.parent.right = w;
            else  root = w;
        }
        return w;
    }

    private AVLNode restructure(AVLNode n) {

        // n is unbalanced
        // returns the node that takes the position of n
        AVLNode p=n.parent,z=n,x=null,y=null,
        a=null,b=null,c=null, t1=null,t2=null;
        // t0 and t3 never change their parent,
        // that's why we don't need them
        if (z.left.height > z.right.height){
            //   z
            //  /
            // y
            c=z;
            y=z.left;
            if (y.left.height >=y.right.height){
                // in case we have two equal branches
                // concidering the length we take alway s the single
                // rotation
                //     z
                //    /
                //   y
                //  /
                // x
                x=y.left;
                t1=x.right;
                t2=y.right;
                b=y;
                a=x;
            }
            else {
                //     z
                //    /
                //   y
                //   \  
                //    x
                x=y.right;
                t1=x.left;
                t2=x.right;
                a=y;
                b=x;
            }
        }
        else{
            // z
            //   \
            //    y
            a=z;
            y=z.right;
            if (y.right.height >= y.left.height){
                //  z
                //   \
                //    y
                //     \  
                //      x
                x=y.right;
                b=y;
                c=x;
                t1=y.left;
                t2=x.left;
            }
            else {
                //  z
                //   \
                //    y
                //    /  
                //   x
                x=y.left;
                b=x;
                c=y;
                t1=x.left;
                t2=x.right;
            }
        }        
        // umhaengen
        b.parent = p;
        if (p != null){
            if (p.left == z) {
                p.left=b;
            }
            else p.right=b;
        }
        else {
            root=b;
        }
        b.right = c;
        b.left = a;
        // und umgekehrt
        a.parent = b;
        c.parent = b;

        // subtrees:
        a.right = t1;
        t1.parent = a;
        c.left = t2;
        t2.parent = c;


        a.height = Math.max(a.left.height, a.right.height)+1;
        c.height = Math.max(c.left.height, c.right.height)+1;
        // now we can calculate the height of b
        b.height = Math.max(b.left.height, b.right.height)+1;
        return b;
    }


    @Override
    public Locator<K, E> closestBefore(K key) {
        if (size==0) return null;
        AVLNode n = root;
        AVLNode found = null;
        while ( ! n.isExternal()){
            int comp = key.compareTo(n.key);
            if (comp < 0) n = n.left;
            else if (comp > 0) n=n.right;
            else {
                found = n;
                n=n.left;
            }            
        }
        if (found != null) return previous(found);
        // we are at a external position
        if (n.isRightChild()) return n.parent;
        return previous(n.parent);
    }



    @Override
    public Locator<K, E> closestAfter(K key) {
        if (size==0) return null;
        AVLNode n = root;
        AVLNode found = null;
        while ( ! n.isExternal()){
            int comp = key.compareTo(n.key);
            if (comp > 0) n = n.right;
            else if (comp < 0) n=n.left;
            else {
                found = n;
                n=n.right;
            }            
        }
        if (found != null) return next(found);
        if (n.isLeftChild()) return n.parent;
        return next(n.parent);
    }


    @Override
    public Locator<K, E> next(Locator<K, E> loc) {
        AVLNode n = checkAndCast(loc);
        if (n.right.isExternal()){
            while(n.isRightChild()) n=n.parent;
            n=n.parent;
        }
        else {
            n=n.right;
            while (! n.left.isExternal()) n=n.left;
        }
        return n;
    }




    @Override
    public Locator<K, E> previous(Locator<K, E> loc) {
        AVLNode n = checkAndCast(loc);
        if (n.left.isExternal()){
            while(n.isLeftChild()) n=n.parent;
            n=n.parent;
        }
        else {
            n=n.left;
            while (! n.right.isExternal()) n=n.right;
        }
        return n;
    }




    @Override
    public Locator<K, E> min() {
        if (size == 0) return null;
        AVLNode n = root;
        while (! n.left.isExternal()) n=n.left;
        return n;
    }




    @Override
    public Locator<K, E> max() {
        if (size == 0) return null;
        AVLNode n = root;
        while (! n.right.isExternal()) n=n.right;
        return n;
    }




    @Override
    public Iterator<Locator<K, E>> sortedLocators() {
        return new Iterator<Locator<K,E>>() {
            AVLNode current = (AVLNode)min();

            @Override
            public boolean hasNext() {
                return current == null;
            }

            @Override
            public Locator<K, E> next() {
                AVLNode ret = current; // this is the next node
                //  by one node:
                if (current.right.isExternal()){
                    while(current.isRightChild()) current=current.parent;
                    current=current.parent;
                }
                else {
                    current=current.right;
                    while (! current.left.isExternal()) current=current.left;
                }
                return ret;
            }
        };
    }

    public void print(){
        if (size>0) prittyPrint(root,"");
    }

    private void print(AVLNode n,String in) {
        if (n.isExternal()) return;
        print(n.right,in+".");
        System.out.println(in+n.key);
        print(n.left,in+".");
    }

    private void prittyPrint(AVLNode r, String in) {
        if (r.isExternal()) return;        
        // right subtree
        int sLen = in.length();
        String inNeu = in;
        if (r.isRightChild()) inNeu = in.substring(0,sLen-2)+"  ";
        prittyPrint(r.right,inNeu+" |");
        // root of the subtree
        String inN = in;
        if (sLen>0) inN = in.substring(0,sLen-1)+"+-";
        else inN = in+"-"; // root of the tree
        if ( ! r.right.isExternal()) System.out.println(inNeu+" |");
        else System.out.println(inNeu);
        System.out.println(inN+r.key()+"(h="+r.height+")"+":"+r.elem+")");
        // left subtree
        inNeu = in;
        if (r.isLeftChild()){
            inNeu = in.substring(0,sLen-2)+"  ";
        }
        prittyPrint(r.left,inNeu+" |");
    }

    public void test(){
        if (root.parent != null) throw new RuntimeException("root has a parent: "+root.parent.key);
        test(root);
    }

    private void test(AVLNode n) {
        if (n.isExternal()) return;
        test(n.left);
        test(n.right);
        if (n.left.parent != n) throw new RuntimeException("chaining incorrect"+n.key);
        if (n.right.parent != n) throw new RuntimeException("chaining incorrec"+n.key);
        if (Math.max(n.left.height,n.right.height)+1!=n.height)
            throw new RuntimeException("Height wrong"+n.key);
        if (n.left.key !=null &&  n.left.key.compareTo(n.key)>0) throw new RuntimeException("order wrong "+n.key);
        if (n.right.key !=null &&  n.right.key.compareTo(n.key)<0) throw new RuntimeException("order wrong "+n.key);
        if (Math.abs(n.left.height-n.right.height)> 1) throw new RuntimeException("unbalanced "+n.key);
        if (n.creator != this) throw new RuntimeException("invalid node: "+n.key);
    }


    public static void main(String[] argv){
        MyAVLTree<Integer, String> t = new MyAVLTree<>();
        Random rand = new Random();
        t.insert(6, "e 6.1");
        t.insert(10, "e 10");
        t.insert(7, "e 7");
        t.insert(7, "e 7.2");
        t.insert(6, "e 6.2 ");
        t.insert(3, "e 3");
        Locator loc = t.insert(1, "e 1");        
        t.insert(6, "e 6.3 ");
        t.insert(4, "e 4");
        t.insert(11, "e 11");
        t.print();
        // loc = t.closestBefore(1);
        System.out.println(t.previous(t.closestBefore(2)));
//        }
//        System.out.println(t.find(6).element());
//        int n  = 1000000;
//        Locator<Integer,String>[] locs = new Locator[n];
//        long time1 = System.nanoTime();
//        for (int i=0;i<n;i++) {
//            locs[i]=t.insert(i,"");
//            //locs[i]=t.insert(i, "bla");
//        }
//        // t.test();
//        for (int i= 0; i<n; i++ ) {
//            t.remove(locs[i]);
//            // t.test();
//        }
//        long time2 = System.nanoTime();
//        System.out.println("ms used: "+(time2-time1)/1e6);
//        System.out.println(t.root.height);
        // System.out.println((t.find(13).element()));
        //  t.print();
//        Locator<Integer,String>
//        loc = t.min();
//        while (loc != null){
//            System.out.println(loc.key());
//            loc = t.next(loc);
//        }
//    }
////    Map s = new TreeMap();
//    for (int i=0;i<n;i++) {
//        s.put(rand.nextInt(),"");
//    }
    }
}