Skip Lists

What is a Skip List

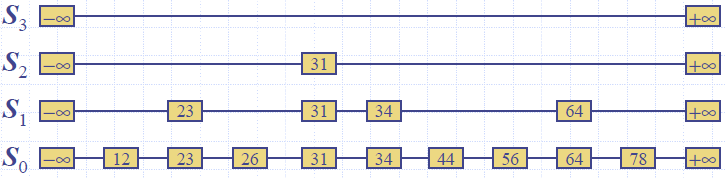
• A skip list for a set S of distinct (key, element) items is a series of lists S0, S1 , … , Sh such that
  • Each list Si contains the special keys +∞ and −∞
  • List S0 contains the keys of S in nondecreasing order
  • Each list is a subsequence of the previous one, i.e., S0 ⊇S1 ⊇ … ⊇ Sh
  • List Sh contains only the two special keys
• We show how to use a skip list to implement the dictionary ADT

Search

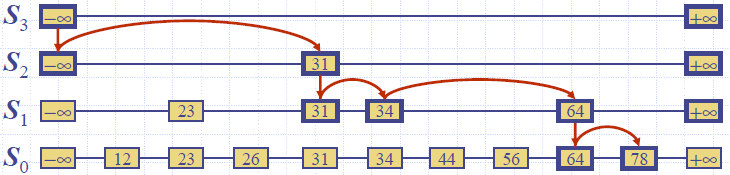
• We search for a key x in a a skip list as follows:
  • We start at the first position of the top list
  • At the current position p, we compare x with y ←key(after(p))
    x = y: we return element(after(p))
    x > y: we “scan forward”
    x < y: we “drop down”
  • If we try to drop down past the bottom list, we return NO_SUCH_KEY
• Example: search for 78

Randomized Algorithms

• A randomized algorithm performs coin tosses (i.e., uses random bits) to control its execution
• It contains statements of the type

  b ← random()
  if b = 0
  do A …
  else { b = 1}
  do B …
  

• Its running time depends on the outcomes of the coin tosses
• We analyze the expected running time of a randomized algorithm under the following assumptions
  • the coins are unbiased, and
  • the coin tosses are independent
• The worst-case running time of a randomized algorithm is often large but has very low probability (e.g., it occurs when all the coin tosses give “heads”)
• We use a randomized algorithm to insert items into a skip list

Insertion

• To insert an item (x, o) into a skip list, we use a randomized algorithm:
  • We repeatedly toss a coin until we get tails, and we denote with i the number of times the coin came up heads
  • If i ≥ h, we add to the skip list new lists Sh+1, … , Si +1, each containing only the two special keys
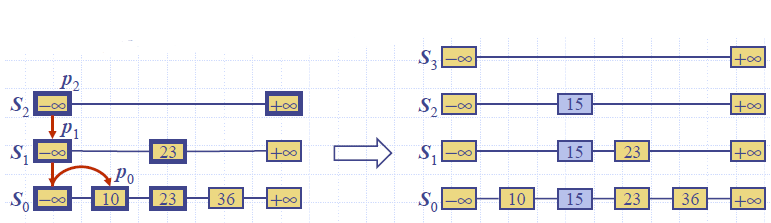
  • We search for x in the skip list and find the positions p0, p1 , …, pi of the items with largest key less than x in each list S0, S1, … , Si
  • For j ← 0, …, i, we insert item (x, o) into list Sj after position pj
• Example: insert key 15, with i = 2

Removal

• To remove an item with key x from a skip list, we proceed as follows:
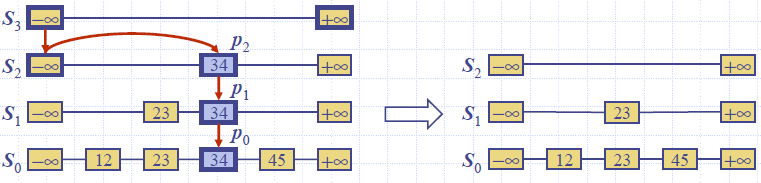
  • We search for x in the skip list and find the positions p0, p1 , …, pi of the items with key x, where position pj is in list Sj
  • We remove positions p0, p1 , …, pi from the lists S0, S1, … , Si
  • We remove all but one list containing only the two special keys
• Example: remove key 34

Height

• The running time of the search an insertion algorithms is affected by the height h of the skip list
• We show that with high probability, a skip list with n items has height O(log n)
• We use the following additional probabilistic fact:
  • Fact 3: If each of n events has probability p, the probability that at least one event occurs is at most np
• Consider a skip list with n items
  • By Fact 1, we insert an item in list Si with probability 1/2^i
  • By Fact 3, the probability that list Si has at least one item is at most n/2^i
• By picking i = 3log n, we have that the probability that S_3log n has at least one item is at most n/2^3log n = n/n³ = 1/n²
• Thus a skip list with n items has height at most 3log n with probability at least 1 − 1/n²

Search and Update Times

• The search time in a skip list is proportional to 􀂄
  • the number of drop-down steps, plus
  • the number of scan-forward steps
• The drop-down steps are bounded by the height of the skip list and thus are O(log n) with high probability
• To analyze the scan-forward steps, we use yet another probabilistic fact:
  • Fact 4: The expected number of coin tosses required in order to get tails is 2
• When we scan forward in a list, the destination key does not belong to a higher list
  • A scan-forward step is associated with a former coin toss that gave tails
• By Fact 4, in each list the expected number of scanforward steps is 2
• Thus, the expected number of scan-forward steps is O(log n)
• We conclude that a search in a skip list takes O(log n) expected time
• The analysis of insertion and deletion gives similar results

Space Usage

• The space used by a skip list depends on the random bits used by each invocation of the insertion algorithm
• We use the following two basic probabilistic facts:
  • Fact 1: The probability of getting i consecutive heads when flipping a coin is 1/2^i
  • Fact 2: If each of n items is present in a set with probability p, the expected size of the set is np
• Consider a skip list with n items
  • By Fact 1, we insert an item in list Si with probability 1/2^i
  • By Fact 2, the expected size of list Si is n/2^i
• The expected number of nodes used by the skip list is
  
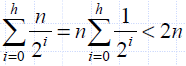
• Thus, the expected space usage of a skip list with n items is O(n)

Summary/Runtime Analysis

• A skip list is a data structure for dictionaries that uses a randomized insertion algorithm
• In a skip list with n items
  • The expected space used is O(n)
  • The expected search, insertion and deletion time is O(log n)
• Using a more complex probabilistic analysis, one can show that these performance bounds also hold with high probability
• Skip lists are fast and simple to implement in practice

Code

/**
 *
 */
package examples;

import java.util.ArrayList;
import java.util.Iterator;
import java.util.Random;



/**
 * @author ps
 *
 */
public class MySkipList<K extends Comparable<? super K>, E> implements
        OrderedDictionary<K, E> {

    // the class for the nodes:
    class SLNode implements Locator<K,E> {
        SLNode prev,next,above,below; // neighbours
        Object owner = MySkipList.this;
        K key;
        E elem;

        /* (non-Javadoc)
         * @see examples.Position#element()
         */
        @Override
        public E element() {
            return elem;
        }

        /* (non-Javadoc)
         * @see examples.Locator#key()
         */
        @Override
        public K key() {
            return key;
        }
    }


    // instance variables
    // 4 inital nodes which remain alway the same
    private SLNode topLeft,bottomLeft,topRight,bottomRight;
    // min, max
    private K minKey,maxKey;
    //
    private int size;
    private Random rand = new Random();
    private double p = 0.5; // index probability
    private int height = 2;

    public MySkipList(K min, K max){
        topLeft = new SLNode();
        topLeft.key = min;
        topRight = new SLNode();
        topRight.key = max;
        bottomLeft = new SLNode();
        bottomLeft.key = min;
        bottomRight = new SLNode();
        bottomRight.key = max;
        // connect them
        topLeft.next = topRight;
        topRight.prev = topLeft;
        bottomLeft.next = bottomRight;
        bottomRight.prev = bottomLeft;

        topLeft.below = bottomLeft;
        topRight.below = bottomRight;
        bottomLeft.above = topLeft;
        bottomRight.above = topRight;

        minKey = min;
        maxKey = max;
    }




    /* (non-Javadoc)
     * @see examples.OrderedDictionary#size()
     */
    @Override
    public int size() {
        return size;
    }

    private void checkKey(K key){
        if (key.compareTo(minKey)<=0) throw new RuntimeException("key not bigger than minKey!");
        if (key.compareTo(maxKey)>=0) throw new RuntimeException("key not smaller than maxKey!");        
    }

    /* (non-Javadoc)
     * @see examples.OrderedDictionary#find(java.lang.Comparable)
     */
    @Override
    public Locator<K, E> find(K key) {
        checkKey(key);
        SLNode pos = search(key);
        if (pos.key.compareTo(key)!=0) return null; // we found nothing
        else {
            // we take the leftmost Locator with valid key
            while (pos.prev.key.compareTo(key)== 0) pos=pos.prev;
            return pos;
        }
    }

    private SLNode search(K key){
        SLNode pos = topLeft;
        while (pos.below != null){
            pos = pos.below;
            while (key.compareTo(pos.next.key) >=0) pos = pos.next;
        }
        return pos;        
    }


    /* (non-Javadoc)
     * @see examples.OrderedDictionary#findAll(java.lang.Comparable)
     */
    @Override
    public Locator<K, E>[] findAll(K key) {
        SLNode n = (SLNode) find(key); // returns the leftmost occurence
        if (n==null) return new Locator[0];
        ArrayList<Locator<K,E>> al = new ArrayList<>();
        while(n.key.compareTo(key)==0){
            al.add(n);
            n=n.next;
        }
        return al.toArray(new Locator[0]);
    }


    /* (non-Javadoc)
     * @see examples.OrderedDictionary#insert(java.lang.Comparable, java.lang.Object)
     */
    @Override
    public Locator<K, E> insert(K key, E o) {
        checkKey(key);
        SLNode pos = search(key);
        // we take the rightmost Locator with valid key
        while (pos.next.key.compareTo(key)== 0) pos=pos.next;        
        // now we want to insert a node at the position pos.next:        
        // make a new node:        
        SLNode nNew = new SLNode();
        nNew.key = key;
        nNew.elem = o;

        // insert at pos.next
        nNew.next = pos.next;
        nNew.prev = pos;
        // backwards chaining:
        nNew.next.prev=nNew;
        nNew.prev.next=nNew;

        // build index:

        SLNode lastIndex = nNew;
        while (rand.nextDouble() < p){
            while (pos.above==null) pos = pos.prev;
            pos = pos.above;
            // create a new index and insert it after pos:
            SLNode index = new SLNode();
            index.key = key;            
            // insert:
            // horizontal chaining:
            index.prev = pos;
            index.next = pos.next;
            index.next.prev = index;
            index.prev.next = index;
            // vertical chaining:
            index.below = lastIndex;
            lastIndex.above = index;        
            // increment  
            lastIndex=index;          
            // if pos is topLeft we have to expand by one index level
            if (pos == topLeft) expand();

        }
        size++;
        return nNew;
    }

    private void expand(){
        // adds one index level
        // System.out.println("expanding..");
        SLNode n1 = new SLNode();
        n1.key = minKey;
        SLNode n2 = new SLNode();
        n2.key = maxKey;
        n1.next = n2;
        n2.prev = n1;

        n1.below = topLeft;
        n2.below = topRight;

        topLeft.above = n1;
        topRight.above = n2;

        topLeft = n1;
        topRight = n2;
        height++;
    }

    /* (non-Javadoc)
     * @see examples.OrderedDictionary#remove(examples.Locator)
     */
    @Override
    public void remove(Locator<K, E> loc) {
        SLNode n = (SLNode) loc;
        if (n.owner != this) throw new RuntimeException("invalid locator "+loc.key());
        n.owner=null;
        int lev=0;
        while (n!=null){
            n.prev.next=n.next;
            n.next.prev=n.prev;
            n=n.above;
            lev++;
        }
        if (lev==height-1) shrink();
        size--;
    }


    /**
     *
     */
    private void shrink() {
        // System.out.println("shrink called");
        while (height>2 && topLeft.below.next==topRight.below){
            // System.out.println("shrinking...");
            topLeft = topLeft.below;
            topRight = topRight.below;
            topLeft.above = null;
            topRight.above = null;
            height--;
        }
    }


    /* (non-Javadoc)
     * @see examples.OrderedDictionary#closestBefore(java.lang.Comparable)
     */
    @Override
    public Locator<K, E> closestBefore(K key) {
        if (key.compareTo(minKey)<=0) throw new RuntimeException("key not bigger than minKey!");
        if (key.compareTo(maxKey)>=0) throw new RuntimeException("key not smaller than maxKey!");
        SLNode pos = search(key);
        int comp = key.compareTo(pos.key);
        if (comp==0){
            pos = pos.prev;
            // still equal?
            if (pos == bottomLeft) return null;
            while (key.compareTo(pos.key)==0) pos=pos.prev;
        }
        else if (comp>0){
            // in case we have sevearal equal keys take the rightmost locator
            while (pos.key.compareTo(pos.next.key)==0) pos=pos.next;
            if (pos == bottomLeft) pos = null;

        }
        else
            throw new RuntimeException("should never happen!");
        return pos;

    }

    /* (non-Javadoc)
     * @see examples.OrderedDictionary#closestAfter(java.lang.Comparable)
     */
    @Override
    public Locator<K, E> closestAfter(K key) {
        if (key.compareTo(minKey)<=0) throw new RuntimeException("key not bigger than minKey!");
        if (key.compareTo(maxKey)>=0) throw new RuntimeException("key not smaller than maxKey!");
        SLNode pos = search(key);
        int comp = key.compareTo(pos.key);
        if (comp==0){
            pos = pos.next;
            // still equal?
            while (key.compareTo(pos.key)==0) pos=pos.next;
            if (pos == bottomRight) pos = null;
        }
        else if (comp>0){
            // in case we have several equal keys take the rightmost locator
            while (pos.key.compareTo(pos.next.key)==0) pos=pos.next;
            // the next key is bigger than 'key'
            pos = pos.next;
            if (pos == bottomRight) pos = null;

        }
        else throw new RuntimeException("should never happen!");
        return pos;
    }


    /* (non-Javadoc)
     * @see examples.OrderedDictionary#next(examples.Locator)
     */
    @Override
    public Locator<K, E> next(Locator<K, E> loc) {
        SLNode n = (SLNode) loc;
        if (n.owner != this) throw new RuntimeException("invalid locator "+loc.key());
        n = n.next;
        if (n==bottomRight) n=null;
        return n;
    }


    /* (non-Javadoc)
     * @see examples.OrderedDictionary#previous(examples.Locator)
     */
    @Override
    public Locator<K, E> previous(Locator<K, E> loc) {
        SLNode n = (SLNode) loc;
        if (n.owner != this) throw new RuntimeException("invalid locator "+loc.key());
        n = n.prev;
        if (n==bottomLeft) n=null;
        return n;
    }


    /* (non-Javadoc)
     * @see examples.OrderedDictionary#min()
     */
    @Override
    public Locator<K, E> min() {
        if (size>0) return bottomLeft.next;
        else return null;
    }


    /* (non-Javadoc)
     * @see examples.OrderedDictionary#max()
     */
    @Override
    public Locator<K, E> max() {
        if (size>0) return bottomRight.prev;
        else return null;
    }


    /* (non-Javadoc)
     * @see examples.OrderedDictionary#sortedLocators()
     */
    @Override
    public Iterator<Locator<K, E>> sortedLocators() {
        return new Iterator<Locator<K, E>>(){
            SLNode pos = bottomLeft.next;
            @Override
            public boolean hasNext() {
                return pos != bottomRight;
            }

            @Override
                public Locator<K, E> next() {
                SLNode ret = pos;
                pos = pos.next;
                return ret;
            }

            @Override
            public void remove() {
                throw new UnsupportedOperationException(
                        "use remove method of MySkipList!");
            }

        };
    }

    public void print(){
        System.out.println("-------start------");
        SLNode n = bottomLeft;
        n=n.next;
        StringBuffer lev = new StringBuffer();
        while (n!=bottomRight){
            lev.delete(0,lev.length());
            SLNode m = n;
            int index = 0;
            while (m.above != null) {
                index++;
                m=m.above;
                lev.append("+");
            }
            while(index<height-2){
                index++;
                lev.append("|");
            }
            System.out.println(String.format("%11d", n.key())+lev.toString()+"    elem: "+n.elem);
            n=n.next;
        }
        System.out.println("--------end-------");

    }


    /**
     * @param args
     */
    public static void main(String[] args) {
        MySkipList<Integer, String> sl = new MySkipList<>(Integer.MIN_VALUE,Integer.MAX_VALUE);
        Random rand = new Random();
        int n  = 1000000;
        Locator<Integer,String>[] locs = new Locator[n];
        long time1 = System.currentTimeMillis();
        for (int i=0;i<n;i++) {
            locs[i]=sl.insert(rand.nextInt(n),""+i);
        }
        for (int i=0;i<n/2;i++) {
            sl.remove(locs[i]);
        }
        Locator<Integer,String>[] ll = sl.findAll(33);
        for (int i=0;i<ll.length;i++)System.out.println(ll[i].key());
        long time2 = System.currentTimeMillis();
        System.out.println("elapsed time: "+(time2-time1)/1000.0+" s");
        System.out.println("height of index: "+sl.height);
//        Iterator<Locator<Integer,String>> it = sl.sortedLocators();
//        while (it.hasNext()){
//            Locator<Integer, String> loc = it.next();
//            System.out.println(loc.key()+" element: "+loc.element());
//        }
        // sl.print();
//        sl.remove(locs[15]);
//        sl.print();
//        Locator<Integer,String> loc = sl.closestBefore(83);
//        if (loc!= null)System.out.println(loc.key()+":"+loc.element());
    }

}