Depth-First Search
Subgraphs
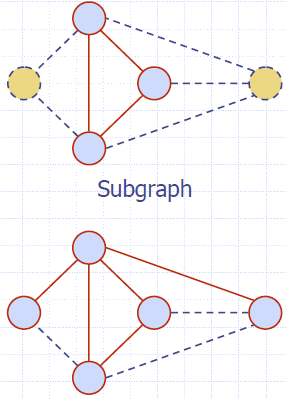
- A subgraph S of a graph G is a graph such that
- The vertices of S are a subset of the vertices of G
- The edges of S are a subset of the edges of G
- A spanning subgraph of G is a subgraph that contains all the vertices of G
Connectivity
- A graph is connected if there is a path between every pair of vertices
- A connected component of a graph G is a maximal connected subgraph of G
Trees and Forests
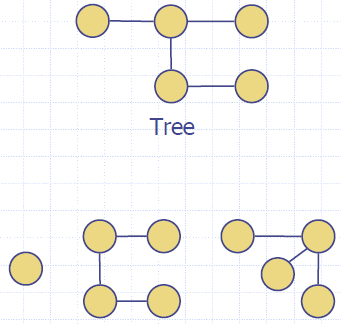
- A (free) tree is an undirected graph T such that
- T is connected
- T has no cycles
This definition of tree is different from the one of a rooted tree
- A forest is an undirected graph without cycles
- The connected components of a forest are trees
Spanning Trees and Forests
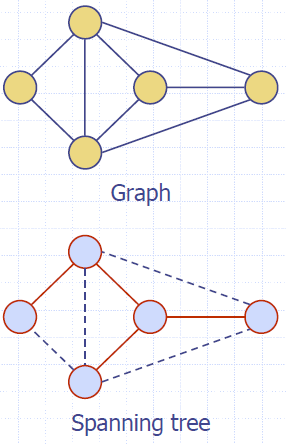
- A spanning tree of a connected graph is a spanning subgraph that is a tree
- A spanning tree is not unique unless the graph is a tree
- Spanning trees have applications to the design of communication networks
- A spanning forest of a graph is a spanning subgraph that is a forest
Depth-First Search
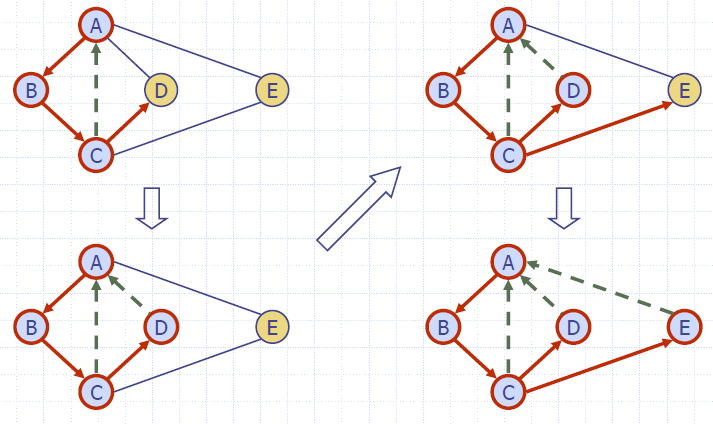
- Depth-first search (DFS) is a general technique for traversing a graph
- A DFS traversal of a graph G
- Visits all the vertices and edges of G
- Determines whether G is connected
- Computes the connected components of G
- Computes a spanning forest of G
- DFS on a graph with n vertices and m edges takes O(n + m ) time
- DFS can be further extended to solve other graph problems
- Find and report a path between two given vertices
- Find a cycle in the graph
- Depth-first search is to graphs what Euler tour is to binary trees
DFS Algorithm
- The algorithm uses a mechanism for setting and getting “labels” of vertices and edges
Algorithm DFS(G)
Input graph G
Output labeling of the edges of G as discovery edges and back edges
for all u ∈ G.vertices()
setLabel(u, UNEXPLORED)
for all e ∈ G.edges()
setLabel(e, UNEXPLORED)
for all v ∈ G.vertices()
if getLabel(v) = UNEXPLORED
DFS(G, v)
Algorithm DFS(G, v)
Input graph G and a start vertex v of G
Output labeling of the edges of G in the connected component of v as discovery edges and back edges
setLabel(v, VISITED)
for all e ∈ G.incidentEdges(v)
if getLabel(e) = UNEXPLORED
w ← G.opposite(v,e)
if getLabel(w) = UNEXPLORED
setLabel(e, DISCOVERY)
DFS(G, w)
else
setLabel(e, BACK)
DFS and Maze Traversal
- The DFS algorithm is similar to a classic strategy for exploring a maze
- We mark each intersection, corner and dead end (vertex) visited
- We mark each corridor (edge ) traversed
- We keep track of the path back to the entrance (start vertex)by means of a rope (recursion stack)
Properties of DFS
- Property 1
- DFS(G, v) visits all the vertices and edges in the connected component of v
- Property 2
- The discovery edges labeled by DFS(G, v) form a spanning tree of the connected component of v
Analysis of DFS
- Setting/getting a vertex/edge label takes O(1) time
- Each vertex is labeled twice
- once as UNEXPLORED
- once as VISITED
- Each edge is labeled twice
- once as UNEXPLORED
- once as DISCOVERY or BACK
- Method incidentEdges is called once for each vertex
- DFS runs in O(n + m) time provided the graph is represented by the adjacency list structure
- Recall that Σv deg(v) = 2m
Path Finding
- We can specialize the DFS algorithm to find a path between two given vertices u and z using the template method pattern
- We call DFS(G, u) with u as the start vertex
- We use a stack S to keep track of the path between the start vertex and the current vertex
- As soon as destination vertex z is encountered, we return the path as the contents of the stack
Algorithm pathDFS(G, v, z)
setLabel(v, VISITED)
S.push(v)
if v = z
return S.elements()
for all e ∈ G.incidentEdges(v)
if getLabel(e) = UNEXPLORED
w ← opposite(v, e)
if getLabel(w) = UNEXPLORED
setLabel(e, DISCOVERY)
S.push(e)
pathDFS(G, w, z)
S.pop() { e gets popped }
else
setLabel(e, BACK)
S.pop() { v gets popped }
Cycle Finding
- We can specialize the DFS algorithm to find a simple cycle using the template method pattern
- We use a stack S to keep track of the path between the start vertex and the current vertex
- As soon as a back edge (v, w) is encountered, we return the cycle as the portion of the stack from the top to vertex w
Algorithm cycleDFS(G, v, z)
setLabel(v, VISITED)
S.push(v)
for all e ∈ G.incidentEdges(v)
if getLabel(e) = UNEXPLORED
w ← opposite(v,e)
S.push(e)
if getLabel(w) = UNEXPLORED
setLabel(e, DISCOVERY)
pathDFS(G, w, z)
S.pop()
else
C ← new empty stack
repeat
o ← S.pop()
C.push(o)
until o = w
return C.elements()
S.pop()
Code
package examples;
import graphLib.*;
import graphTool.Algorithm;
import graphTool.Attribute;
import graphTool.GraphTool;
import java.awt.Color;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Random;
public class GraphExamples<V,E> {
@Algorithm(vertex=true,vertex2=true)
public void findPath(Graph<V,E> g, Vertex<V> v,Vertex<V> v2, GraphTool<V,E> t) {
LinkedList<Vertex<V>> list = new LinkedList<>();
v.set(Attribute.color,Color.BLUE);
v2.set(Attribute.color,Color.RED);
v.set(Attribute.VISITED,null);
t.show(g);
list.addLast(v);
while (! list.isEmpty()){
Vertex w = list.removeFirst();
Iterator<Edge<E>> it = g.incidentEdges(w);
while (it.hasNext()){
Edge e = it.next();
Vertex n = g.opposite(e, w);
if ( ! n.has(Attribute.VISITED)){
n.set(Attribute.VISITED,null);
n.set(Attribute.DISCOVERY,e);
if (n==v2) break;
list.addLast(n);
}
}
if (v2.has(Attribute.DISCOVERY)) break;
}
while (v2.has(Attribute.DISCOVERY)){
Edge e = (Edge) v2.get(Attribute.DISCOVERY);
e.set(Attribute.color,Color.green);
t.show(g);
v2 = g.opposite(e, v2);
}
}
@Algorithm(vertex=true)
public void visitDFS2(Graph<V,E> g, Vertex<V> v, GraphTool<V,E> t) {
LinkedList<Vertex<V>> list = new LinkedList<>();
v.set(Attribute.color,Color.BLUE);
v.set(Attribute.DISCOVERY,null);
list.addLast(v);
t.show(g);
while (! list.isEmpty()){
Vertex w = list.removeLast();
if ( ! w.has(Attribute.VISITED)){
Edge de = (Edge) (w.get(Attribute.DISCOVERY));
if (de!=null) de.set(Attribute.color,Color.green);
w.set(Attribute.VISITED,null);
w.set(Attribute.color,Color.GREEN);
t.show(g);
Iterator<Edge<E>> it = g.incidentEdges(w);
while (it.hasNext()){
Edge e = it.next();
Vertex n = g.opposite(e, w);
if (! n.has(Attribute.VISITED)){
n.set(Attribute.DISCOVERY,e);
list.addLast(n);
}
}
}
}
}
@Algorithm(vertex=true)
public void visitDFS(Graph<V,E> g, Vertex<V> v, GraphTool<V,E> t) {
v.set(Attribute.VISITED,null);
v.set(Attribute.color,Color.green);
t.show(g);
Iterator<Edge<E>> it = g.incidentEdges(v);
while (it.hasNext()){
Edge<E> e = it.next();
Vertex<V> w = g.opposite(e, v);
if ( ! w.has(Attribute.VISITED)) {
e.set(Attribute.color,Color.green);
visitDFS(g,w,t);
}
}
}
public static void main(String[] args) {
IncidenceListGraph<String,String> g =
new IncidenceListGraph<>(true);
GraphExamples<String,String> ge = new GraphExamples<>();
Vertex vA = g.insertVertex("A");
vA.set(Attribute.name,"A");
Vertex vB = g.insertVertex("B");
vB.set(Attribute.name,"B");
Vertex vC = g.insertVertex("C");
vC.set(Attribute.name,"C");
Vertex vD = g.insertVertex("D");
vD.set(Attribute.name,"D");
Vertex vE = g.insertVertex("E");
vE.set(Attribute.name,"E");
Vertex vF = g.insertVertex("F");
vF.set(Attribute.name,"F");
Vertex vG = g.insertVertex("G");
vG.set(Attribute.name,"G");
Edge e_a = g.insertEdge(vA,vB,"AB");
Edge e_b = g.insertEdge(vD,vC,"DC");
Edge e_c = g.insertEdge(vD,vB,"DB");
Edge e_d = g.insertEdge(vC,vB,"CB");
Edge e_e = g.insertEdge(vC,vE,"CE");
e_e.set(Attribute.weight,2.0);
Edge e_f = g.insertEdge(vB,vE,"BE");
e_f.set(Attribute.weight, 7.0);
Edge e_g = g.insertEdge(vD,vE,"DE");
Edge e_h = g.insertEdge(vE,vG,"EG");
e_h.set(Attribute.weight,3.0);
Edge e_i = g.insertEdge(vG,vF,"GF");
Edge e_j = g.insertEdge(vF,vE,"FE");
GraphTool t = new GraphTool(g,ge);
}
}