(2,4) Trees

Multi-Way Search Tree

  • A multi-way search tree is an ordered tree such that
    • Each internal node has at least two children and stores d −1 key-element items (ki, oi), where d is the number of children
    • For a node with children v1 v2…vd storing keys k1 k2 …kd−1
    • keys in the subtree of v1 are less than k1
    • keys in the subtree of vi are between ki−1 and ki (i = 2, …, d − 1)
    • keys in the subtree of vd are greater than kd−1
  • The leaves store no items and serve as placeholders

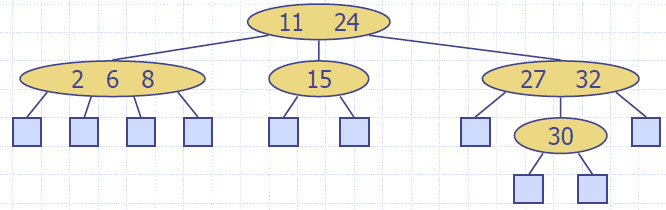
Multiway_Search_Tree

Multi-Way Inorder Traversal

  • We can extend the notion of inorder traversal from binary trees to multi-way search trees
  • Namely, we visit item (ki, oi) of node v between the recursive traversals of the subtrees of v rooted at children vi and vi + 1
  • An inorder traversal of a multi-way search tree visits the keys in increasing order

Multiway_Search_Tree

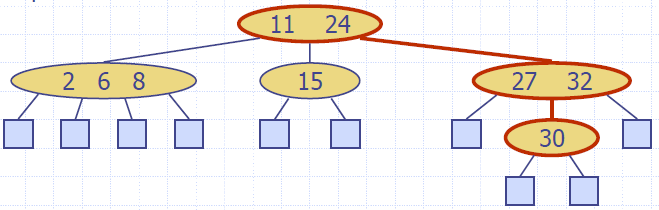
Searching

  • Similar to search in a binary search tree
  • A each internal node with children v1 v2 …vd and keys k1 k2 …kd−1
    • k = ki (i = 1, …, d − 1): the search terminates successfully
    • k < k1: we continue the search in child v1
    • ki−1 < k < ki (i = 2, …, d − 1): we continue the search in child vi
    • k > kd−1: we continue the search in child vd
  • Reaching an external node terminates the search unsuccessfully
  • Example: search for 30

Multiway_Search_Tree_Search

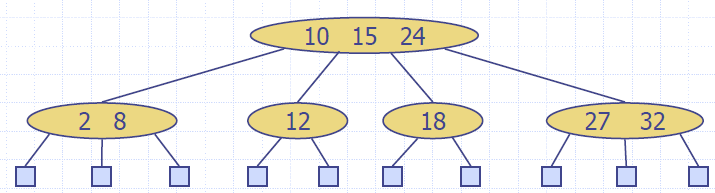
(2,4) Tree

  • A (2,4) tree (also called 2-4 tree or 2-3-4 tree) is a multi-way search with the following properties:
    • Node-Size Property: every internal node has at most four children
    • Depth Property: all the external nodes have the same depth
  • Depending on the number of children, an internal node of a (2,4) tree is called a 2-node, 3-node or 4-node

2_4_Tree.PNG

Height of a (2,4) Tree

  • Theorem: A (2,4) tree storing n items has height O(log n)
  • Proof:
    • Let h be the height of a (2,4) tree with n items
    • Since there are at least 2i items at depth i = 0, … , h − 1 and no items at depth h, we have n ≥ 1 + 2 + 4 +… + 2h−1 = 2h − 1
    • Thus, h ≤ log (n + 1)
  • Searching in a (2,4) tree with n items takes O(log n) time

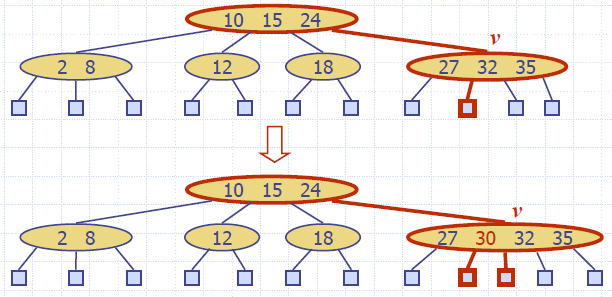
Insertion

  • We insert a new item (k, o) at the parent v of the leaf reached by searching for k
    • We preserve the depth property but
    • We may cause an overflow (i.e., node v may become a 5-node)
  • Example: inserting key 30 causes an overflow

2_4_Tree_Insert

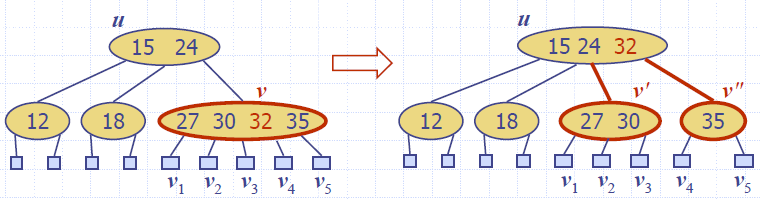
Overflow and Split

  • We handle an overflow at a 5-node v with a split operation:
    • let v1 … v5 be the children of v and k1 … k4 be the keys of v
    • node v is replaced nodes v' and v"
      • v' is a 3-node with keys k1 k2 and children v1 v2 v3
      • v" is a 2-node with key k4 and children v4 v5
    • key k3 is inserted into the parent u of v (a new root may be created)
  • The overflow may propagate to the parent node u

2_4_Tree_Insert_Split

Analysis of Insertion

  • Let T be a (2,4) tree with n items
    • Tree T has O(log n) height
    • Step 1 takes O(log n) time because we visit O(log n) nodes
    • Step 2 takes O(1) time
    • Step 3 takes O(log n) time because each split takes O(1) time and we perform O(log n) splits
  • Thus, an insertion in a (2,4) tree takes O(log n) time
Algorithm insertItem(k, o)
  1. We search for key k to locate the insertion node v
  2. We add the new item (k, o) at node v
  3. while overflow(v)
    if isRoot(v)
      create a new empty root above v
    v ← split(v)

Removal

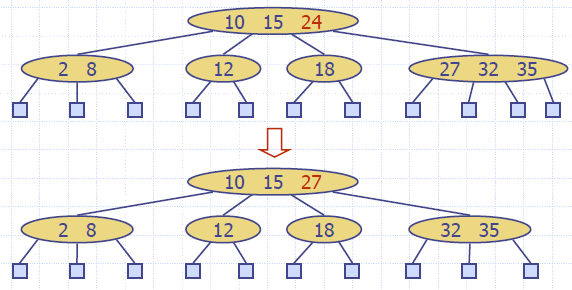
  • We reduce deletion of an item to the case where the item is at the node with leaf children
  • Otherwise, we replace the item with its inorder successor (or, equivalently, with its inorder predecessor) and delete the latter item
  • Example: to delete key 24, we replace it with 27 (inorder successor)

2_4_Tree_Deletion

Underflow and Fusion/Transfer

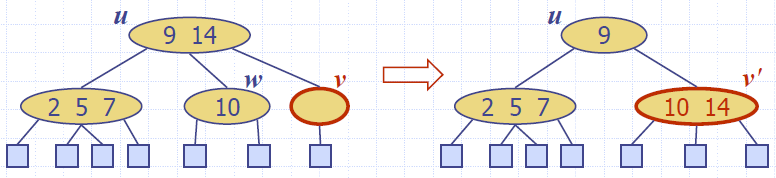
  • Deleting an item from a node v may cause an underflow, where node v becomes a 1-node with one child and no keys
  • To handle an underflow at node v with parent u, we consider two cases
    • Case 1: the adjacent siblings of v are 2-nodes
      • Fusion operation: we merge v with an adjacent sibling w and move an item from u to the merged node v'
      • After a fusion, the underflow may propagate to the parent u
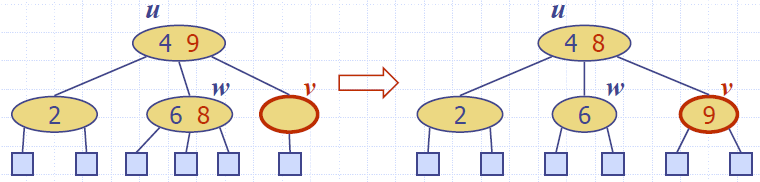
    • Case 2: an adjacent sibling w of v is a 3-node or a 4-node
      • Transfer operation:
        1. we move a child of w to v
        2. we move an item from u to v
        3. we move an item from w to u
      • After a transfer, no underflow occurs

2_4_Tree_Deletion_Fusion

2_4_Tree_Deletion_Transfer

Analysis of Deletion

  • Let T be a (2,4) tree with n items
    • Tree T has O(log n) height
  • In a deletion operation
    • We visit O(log n) nodes to locate the node from which to delete the item
    • We handle an underflow with a series of O(log n) fusions, followed by at most one transfer
    • Each fusion and transfer takes O(1) time
  • Thus, deleting an item from a (2,4) tree takes O(log n) time

Code