Graph Additions

Kruskal's Algorithm

  • The vertices are partitioned into clouds
    • We start with one cloud per vertex
    • Clouds are merged during the execution of the algorithm
  • Partition ADT:
    • makeSet(o): create set {o} and return a locator for object o
    • find(l): return the set of the object with locator l
    • union(A,B): merge sets A and B
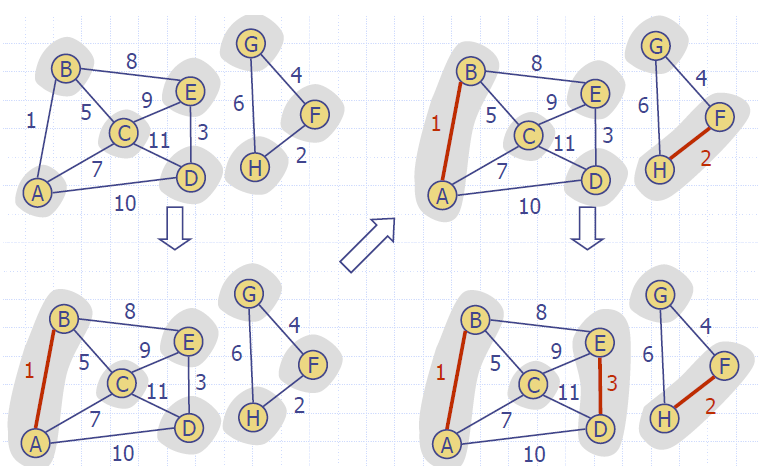
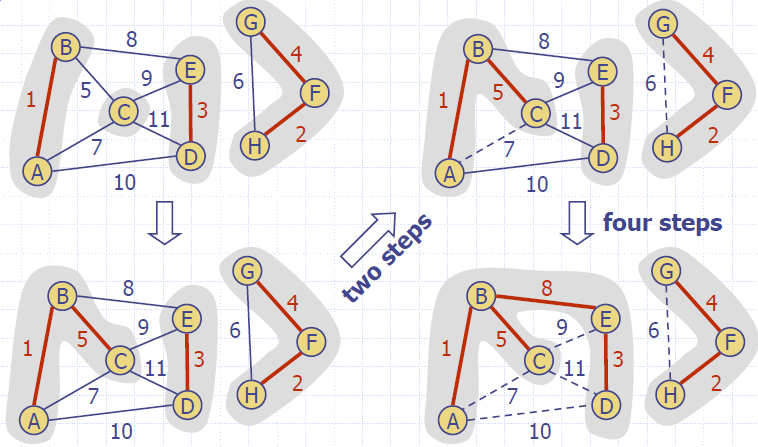
Algorithm KruskalMSF(G)
  Input weighted graph G
  Output labeling of the edges of a minimum spanning forest of G
  Q ← new heap-based priority queue
  for all v ∈ G.vertices() do
    l ← makeSet(v) { elementary cloud }
    setLocator(v,l)
  for all e ∈ G.edges() do
    Q.insert(weight(e), e)
  while ¬Q.isEmpty()
    e ← Q.removeMin()
    [u,v] ← G.endVertices(e)
    A ← find(getLocator(u))
    B ← find(getLocator(v))
    if A ≠ B
      setMSFedge(e)
      { merge clouds }
      union(A, B)

Kurskal

Kurskal

Code

package examples;
import graphLib.*;
import graphTool.Algorithm;
import graphTool.Attribute;
import graphTool.GraphTool;

import java.awt.Color;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Random;


public class GraphExamples<V,E> {
    @Algorithm
    public void kruskal(Graph<V,E> g, GraphTool<V, E> t){
        // gives the Attribute MSF to each
        // edge belonging to an minimal spanning forest

        // create clusters, put the vertex in it  
        // and assign them to the vertice
        Iterator<Vertex<V>> it = g.vertices();
        while(it.hasNext()){
            Vertex v =it.next();
            ArrayList<Vertex<V>> cluster = new ArrayList<>();
            cluster.add(v);
            v.set(Attribute.CLUSTER,cluster);
        }
        PriorityQueue<Double,Edge<E>> pq = new MyPriorityQueue<>();     
        Iterator<Edge<E>> eit = g.edges();
        while(eit.hasNext()){
            Edge e = eit.next();
            double weight = 1;
            if (e.has(Attribute.weight)) weight=(Double)e.get(Attribute.weight);
            pq.insert(weight, e);
        }
        while (! pq.isEmpty()){
            Edge e = pq.removeMin().element();
            Vertex[] endPts = g.endVertices(e);
            ArrayList<Vertex> cluster0 = (ArrayList)endPts[0].get(Attribute.CLUSTER);
            ArrayList<Vertex> cluster1 = (ArrayList)endPts[1].get(Attribute.CLUSTER);
            if (cluster1 != cluster0){
                // we found an MSF edge
                e.set(Attribute.color,Color.GREEN);
                t.show(g);
                for(Vertex w:cluster1){
                    cluster0.add(w);
                    w.set(Attribute.CLUSTER,cluster0);
                }
            }

        }


    }    

    /**
     * @param args
     * 
     */
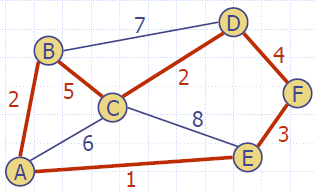
    public static void main(String[] args) {

        //         make an undirected graph
        IncidenceListGraph<String,String> g = 
                new IncidenceListGraph<>(true);
        GraphExamples<String,String> ge = new GraphExamples<>();
        Vertex vA = g.insertVertex("A");
        vA.set(Attribute.name,"A");
        Vertex vB = g.insertVertex("B");
        vB.set(Attribute.name,"B");
        Vertex vC = g.insertVertex("C");
        vC.set(Attribute.name,"C");
        Vertex vD = g.insertVertex("D");
        vD.set(Attribute.name,"D");
        Vertex vE = g.insertVertex("E");
        vE.set(Attribute.name,"E");
        Vertex vF = g.insertVertex("F");
        vF.set(Attribute.name,"F");
        Vertex vG = g.insertVertex("G");
        vG.set(Attribute.name,"G");

        Edge e_a = g.insertEdge(vA,vB,"AB");
        Edge e_b = g.insertEdge(vD,vC,"DC");
        Edge e_c = g.insertEdge(vD,vB,"DB");
        Edge e_d = g.insertEdge(vC,vB,"CB");
        Edge e_e = g.insertEdge(vC,vE,"CE");
        e_e.set(Attribute.weight,2.0);
        Edge e_f = g.insertEdge(vB,vE,"BE"); 
        e_f.set(Attribute.weight, 7.0); 
        Edge e_g = g.insertEdge(vD,vE,"DE");
        Edge e_h = g.insertEdge(vE,vG,"EG");
        e_h.set(Attribute.weight,3.0);
        Edge e_i = g.insertEdge(vG,vF,"GF");
        Edge e_j = g.insertEdge(vF,vE,"FE");
        GraphTool t = new GraphTool(g,ge);

        //    A__B     F
        //      /|\   /|
        //     / | \ / |
        //    C__D__E__G   
        //    \     /
        //     \___/
        //   
    }
}

Partition Implementation

  • Partition implementation
    • A set is represented the sequence of its elements
    • A position stores a reference back to the sequence itself (for operation find)
    • The position of an element in the sequence serves as locator for the element in the set
    • In operation union, we move the elements of the smaller sequence into to the larger sequence
  • Worst-case running times
    • makeSet, find: O(1)
    • union: O(min(nA, nB))
  • Amortized analysis
    • Consider a series of k Partiton ADT operations that includes n makeSet operations
    • Each time we move an element into a new sequence, the size of its set at least double
    • An element is moved at most log2 n times
    • Moving an element takes O(1) time
    • The total time for the series of operations is O(k + n log n)

Analysis of Kruskal’s Algorithm

  • Graph operations
    • Methods vertices and edges are called once
    • Method endVertices is called m times
  • Priority queue operations
    • We perform m insert operations and m removeMin operations
  • Partition operations
    • We perform n makeSet operations, 2m find operations and no more than n − 1 union operations
  • Label operations
    • We set vertex labels n times and get them 2m times Kruskal’s algorithm runs in time O((n + m) log n) time provided the graph has no parallel edges and is represented by the adjacency list structure

Decorator Pattern

  • Labels are commonly used in graph algorithms
    • Auxiliary data
    • Output
  • Examples
    • DFS: unexplored/visited label for vertices and unexplored/ forward/back labels for edges
    • Dijkstra and Prim-Jarnik: distance, locator, and parent labels for vertices
    • Kruskal: locator label for vertices and MSF label for edges
  • The decorator pattern extends the methods of the Position ADT to support the handling of attributes (labels)
    • has(a): tests whether the position has attribute a
    • et(a): returns the value of attribute a
    • set(a, x): sets to x the value of attribute a
    • destroy(a): removes attribute a and its associated value (for cleanup purposes)
  • The decorator pattern can be implemented by storing a dictionary of (attribute, value) items at each position

Traveling Salesperson Problem

  • A tour of a graph is a spanning cycle (e.g., a cycle that goes through all the vertices)
  • A traveling salesperson tour of a weighted graph is a tour that is simple (i.e., no repeated vertices or edges) and has has minimum weight
  • No polynomial-time algorithms are known for computing traveling salesperson tours
  • The traveling salesperson problem (TSP) is a major open problem in computer science
  • Find a polynomial-time algorithm computing a traveling salesperson tour or prove that none exists

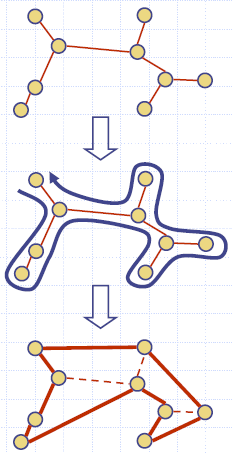
Additions_Traveling_Sales_Person_Problem

TSP Approximation

  • We can approximate a TSP tour with a tour of at most twice the weight for the case of Euclidean graphs
    • Vertices are points in the plane
    • Every pair of vertices is connected by an edge
    • The weight of an edge is the length of the segment joining the points
  • Approximation algorithm
    • Compute a minimum spanning tree
    • Form an Eulerian circuit around the MST
    • Transform the circuit into a tour

Additions_Traveling_Sales_Person_Problem