Red-Black Trees

From (2,4) to Red-Black Trees

• A red-black tree is a representation of a (2,4) tree by means of a binary tree whose nodes are colored red or black
• In comparison with its associated (2,4) tree, a red-black tree has
  • same logarithmic time performance
  • simpler implementation with a single node type
• A red-black tree can also be defined as a binary search tree that satisfies the following properties:
  • Root Property: the root is black
  • External Property: every leaf is black
  • Internal Property: the children of a red node are black
  • Depth Property: all the leaves have the same black depth

Height of a (2,4) Tree

• Theorem: A red-black tree storing n items has height O(log n)
• Proof: The height of a red-black tree is at most twice the height of its associated (2,4) tree, which is O(log n)
• The search algorithm for a binary search tree is the same as that for a binary search tree
• By the above theorem, searching in a red-black tree takes O(log n) time

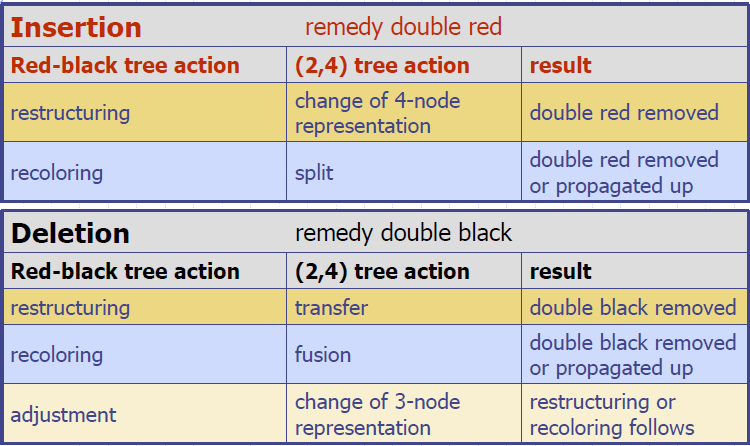
Insertion

• To perform operation insertItem(k, o), we execute the insertion algorithm for binary search trees and color red the newly inserted node z unless it is the root
  • We preserve the root, external, and depth properties
  • If the parent v of z is black, we also preserve the internal property and we are done
    • Else (v is red ) we have a double red (i.e., a violation of the internal property), which requires a reorganization of the tree
• Example where the insertion of 4 causes a double red:

Remedying a Double Red

• Consider a double red with child z and parent v, and let w be the sibling of v
  • Case 1: w is black
    • The double red is an incorrect replacement of a 4-node
    • Restructuring: we change the 4-node replacement
  • Case 2: w is red
    • The double red corresponds to an overflow
    • Recoloring: we perform the equivalent of a split

Analysis of Insertion

• Let T be a (2,4) tree with n items
  • Tree T has O(log n) height
  • Step 1 takes O(log n) time because we visit O(log n) nodes
  • Step 2 takes O(1) time
  • Step 3 takes O(log n) time because each split takes O(1) time and we perform O(log n) splits
• Thus, an insertion in a (2,4) tree takes O(log n) time

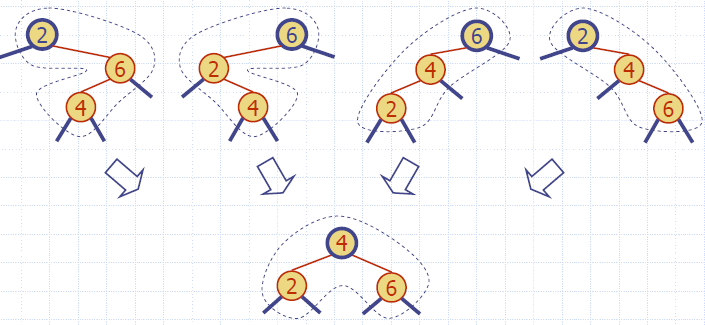
Restructuring

• A restructuring remedies a child-parent double red when the parent red node has a black sibling
• It is equivalent to restoring the correct replacement of a 4-node
• The internal property is restored and the other properties are preserved

• There are four restructuring configurations depending on whether the double red nodes are left or right children

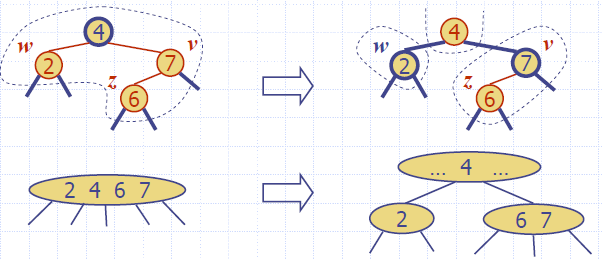
Recoloring

• A recoloring remedies a child-parent double red when the parent red node has a red sibling
• The parent v and its sibling w become black and the grandparent u becomes red, unless it is the root
• It is equivalent to performing a split on a 5-node
• The double red violation may propagate to the grandparent u

Analysis of Insertion

• Recall that a red-black tree has O(log n) height
• Step 1 takes O(log n) time because we visit O(log n) nodes
• Step 2 takes O(1) time
• Step 3 takes O(log n) time because we perform
  • O(log n) recolorings, each taking O(1) time, and
  • a most one restructuring taking O(1) time
• Thus, an insertion in a redblack tree takes O(log n) time

Algorithm insertItem(k, o)
  1. We search for key k to locate the insertion node z
  2. We add the new item (k, o) at node z and color z red
  3. while doubleRed(z)
      if isBlack(sibling(parent(z)))
        z ← restructure(z)
        return
      else { sibling(parent(z) is red }
        z ← recolor(z)

Removal

• To perform operation remove(k), we first execute the deletion algorithm for binary search trees
• Let v be the internal node removed, w the external node removed, and r the sibling of w
  • If either v of r was red, we color r black and we are done
  • Else (v and r were both black) we color r double black, which is a violation of the internal property requiring a reorganization of the tree
• Example where the deletion of 8 causes a double black:

Remedying a Double Black

• The algorithm for remedying a double black node w with sibling y considers three cases
  • Case 1: y is black and has a red child
    • We perform a restructuring, equivalent to a transfer , and we are done
  • Case 2: y is black and its children are both black
    • We perform a recoloring, equivalent to a fusion, which may propagate up the double black violation
  • Case 3: y is red
    • We perform an adjustment, equivalent to choosing a different representation of a 3-node, after which either Case 1 or Case 2 applies
• Deletion in a red-black tree takes O(log n) time

Red-Black Tree Reorganization